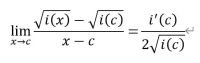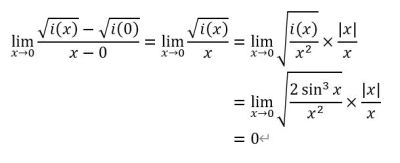수학 가형 190621
조무위키
계속하면 정신이 나가 샷건을 칠 수 있으니 하기 전에 다량의 항암제를 준비하거나 전문가와 상의를 권고합니다. 하지만 이미 늦었군요, YOU DIED |

|

|
이 문서는 이해하기 어려운 대상을 다룹니다. 이 문서는 일반적인 뇌를 가지고도 이해하기 어려운 대상에 대해 다룹니다. 두뇌를 풀가동해도 아마 이해하기 어려울 것입니다. |

|
개요[편집]
2019학년도 6월 평가원 모의고사 21번 문항이다.
역대 평가원 모의고사 21번 문항 중에서는 2018학년도 6평 가형 21번 문제와 함께 가장 어려운 문제로 평가받는다.
문제분석[편집]
f(x)에 대해서[편집]
열린 구간.... f(x)... 가 있다.
일단 f(x)는 정해진 구간에서 완벽하게 정의된 함수이다.
g(t)에 대해서[편집]
실수 t에 대하여 다음 조건을 만족시키는 모든 실수 k의 개수를 g(t)라 하자...
실수 t가 먼저 태어나고 그 다음에 k가 태어났다. 즉 t에 따라서 k가 변동하는 모양새인가 보다.
그 다음에 그 k의 개수를 g(t)라고 하니 t에 따라서 k의 개수의 변화를 봐주면 되겠다.
구하라는 것[편집]
h ∘ g(t) 가 실수 전체의 집합에서 연속이 되도록 하는 최고차항의 계수가 1인 사차함수...
h(x)에 g(t)를 합성한 함수는 실수 전체 구간에서 연속이 되어야한다고 한다.
그리고 최고차항 계수가 1인 사차함수라니까 등식조건을 4개를 구하면 h(x)를 확정시켜볼 수 있겠다.
그리고 마지막엔 g(t)에 특정 값을 넣고 얻은 결과값을 h(x)에 다시 집어 넣어서 답으로 구하라고 한다.
결론은 조건을 통해서 g(t) h(x)의 함수를 낱낱이 파헤치는게 우리의 목적이 되겠다.
조건 분석[편집]
(가) 조건[편집]
- π2 < k < 3π2
k의 범위를 주어줬다. 아까 확인했다시피 k값은 t값에 따라 달라지는데 그 와중에서도 범위를 제약시켜 준 셈이다.
(나) 조건[편집]
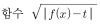 는 x = k에서 미분가능하지 않다.
는 x = k에서 미분가능하지 않다.
미분가능성을 따지는 것의 기본은 미분계수의 정의식을 써놓고 극한을 보내서 그 결과값을 따져보는 것이 정석이다.
즉 등식의 값을 따지는 것. 아까 씨부리던 것과는 다르게 드디어 뭔가 등식조건이 튀어나왔다. 우리는 이제 (나)조건을 분석하는 것으로 문제풀이를 시작할 것이다.
풀이[편집]
Phase 1[편집]
우선 (나)조건을 따지려고 보니 우리가 미분가능성을 조사해야할 식에서 루트 안에 절댓값이 씌워져 있다.
절댓값은 없애주는게 좋으므로 우린 f(x)의 함수값에 따라서 t를 경우에 따라 나누어줄 필요가 있다.
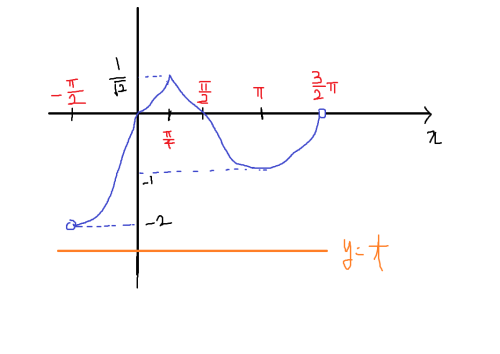
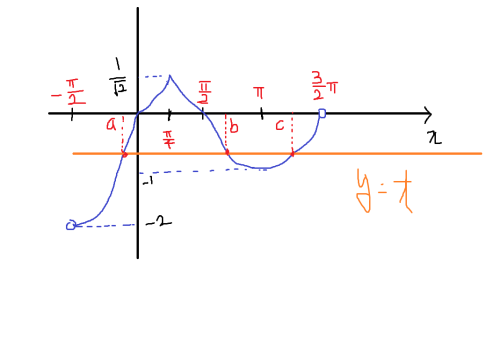
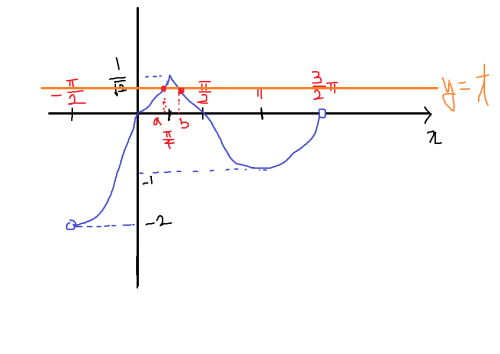
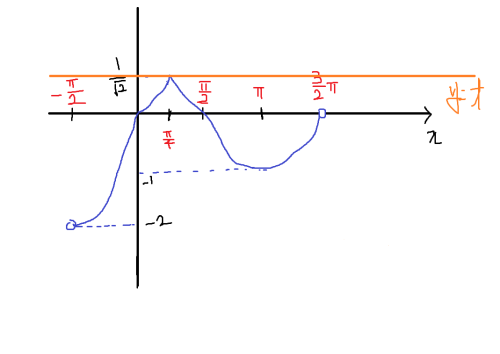
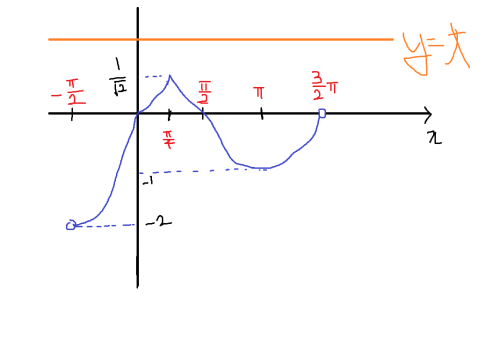
일단 f(x)의 그래프 부터 그려보자. 열심히 그려보면 다음과 같다.
x = - π2, x = 3π2는 함수값이 뚫려있으니까 제외하고 t를 경우에 따라 나누어 보면,
( t ≤ -2 )
( -2 < t < -1 )
( t = -1 )
( -1 < t < 0 )
( 0 ≤ t < 12 √ )
( t = 12 √ )
( t > 12 √ )
정도로 나누어 볼 수 있겠다. 하나씩 따져보자.
(i) ( t ≤ -2 )[편집]
f(x) > t 이므로,
미분가능성 조사를 해야할 식의 루트 안 절댓값 |f(x) - t| = f(x) - t 로 풀린다.
i(x) = f(x) - t라고 하자.
x ≠ π4인 점에서 우선 조사해보자.
x ≠ π4을 만족하는 x = c에서 미분가능성을 조사한다고 했을 때,
위와 같이 미분법 공식을 이용해서 조사를 하면 된다.
i(x) ≠ 0 이고, i'(x) = f'(x)이므로 평균변화율의 좌극한과 우극한이 같음을 알 수 있다.
따라서 x ≠ π4인 점에서는 미분이 가능하다.
이제 x = π4에서는 좌극한, 우극한의 계산에서 f(x)의 함수가 바뀌니까 조사하자.
p(x) = 2sin3x - t
q(x) = cosx - t
p'(x) = 6sin2xcosx
q'(x) = - sinx
라고 하면,
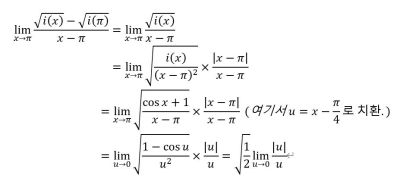
lim(x->π4-)i(x) √ - i(π4) √x - π4 = lim(x->π4-)p(x) √ - p(π4) √x - π4 = p'(π4)2p(π4) √ = -122i(π4) √
lim(x->π4+)i(x) √ - i(π4) √x - π4 = lim(x->π4+)q(x) √ - q(π4) √x - π4 = q'(π4)2q(π4) √ = 322i(π4) √
평균변화율의 좌극한과 우극한의 값이 다르므로, x = π4에서 미분 불가능하다.
종합하면
(t ≤ -2)에서 g(t) = 1이다.
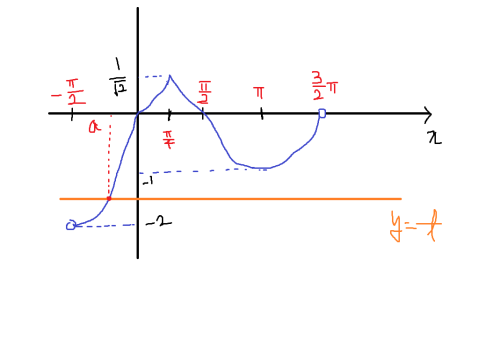
(ii) ( -2 < t < -1 )[편집]
x ≠ π4, a인 모든 실수 x에 대해서는 미분이 가능하다.
(i)에서 확인했듯이, x = π4에서는 미분이 불가능하다.
x = a에서 미분가능성을 조사해보자.
i(x) = f(x) - t 라고 하자. i(a) = 0이다.
평균변화율의 좌극한과 우극한의 값이 발산한다. 따라서, x = a에서 미분 불가능하다.
종합하면
( -2 < t < -1 )에서 g(t) = 2이다.
(iii) ( t = -1 )[편집]
x ≠ π4, a, π인 모든 실수 x에 대해서는 미분이 가능하다.
(i)에서 확인했듯이, x = π4에서는 미분이 불가능하다.
(ii)에서 확인했듯이, x = a에서는 미분이 불가능하다.
x = π에서 미분가능성을 조사해보자.
i(x) = f(x) - t 라고 하자. 이때, i(π) = 0이 된다.
<오타 : u = x-π 로 치환이다.>
평균변화율의 좌극한 = - 12 √, 우극한 = 12 √으로
평균변화율의 좌극한과 우극한의 값이 달라지므로, x = π에서 미분 불가능하다.
종합하면
( t = -1 )에서 g(t) = 3이다.
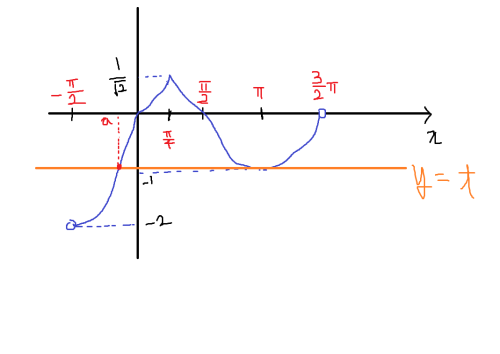
(iv) ( -1 < t < 0 )[편집]
x ≠ π4, a, b, c인 모든 실수 x에 대해서는 미분이 가능하다.
(i)에서 확인했듯이, x = π4에서는 미분이 불가능하다.
(ii)에서 확인했듯이, x = a에서는 미분이 불가능하다.
(ii)에서 x = a를 조사할 때와 같은 논리를 적용하면, x = b, c 에서도 미분이 불가능함을 알 수 있다.
종합하면
( -1 < t < 0 )에서 g(t) = 4이다.
(v) ( t = 0 )[편집]
x ≠ 0, π4, a인 모든 실수 x에 대해서는 미분이 가능하다. (사실 여기서는 a =π2 이다.)
(i)에서 확인했듯이, x = π4에서는 미분이 불가능하다.
(ii)에서 확인할 수 있듯이, x = a에서는 미분이 불가능하다.
x = 0에서의 미분가능성을 조사해보자.
i(x) = f(x) - t 라고 하자. 이때, i(0) = 0이 된다.
평균변화율의 좌극한과 우극한의 값이 0으로 같으므로, x = 0에서 미분 가능하다.
종합하면
( t = 0 )에서 g(t) = 2이다.
(vi) ( 0 < t < 12 √ )[편집]
x ≠ π4, a, b인 모든 실수 x에 대해서는 미분이 가능하다.
(i)에서 확인했듯이, x = π4에서는 미분이 불가능하다.
(ii)에서 확인할 수 있듯이, x = a, b에서는 미분이 불가능하다.
종합하면
( 0 < t < 12 √ )에서 g(t) = 3 이다.
(vii) ( t = 12 √ )[편집]
x ≠ π4인 모든 실수 x에 대해서는 미분이 가능하다.
(i)에서 확인할 수 있듯이, 어차피 x = π4를 경계로 f(x)자체가 완전히 다른 함수로 교체되기 때문에, 상수를 하나 뺀다고해서, 미분불가능점이 가능하게 되지는 않는다.
종합하면
( t = 12 √ )에서 g(t) = 1이다.
(viii) ( t > 12 √ )[편집]
f(x) < t 이므로,
미분가능성 조사를 해야할 식의 루트 안 절댓값 |f(x) - t| = - f(x) + t 로 풀린다.
i(x) = - f(x) + t √라고 하자.
나머지는 (i)의 경우와 같이 x = π4에서만 미분가능성을 조사해주면 된다.
평균변화율의 좌극한과 우극한의 값이 다르므로, x = π4에서 미분 불가능하다.
종합하면
( t > 12 √ )에서 g(t) = 1이다.
Phase 2[편집]
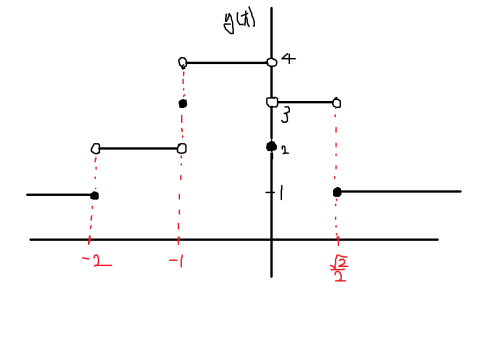
지금까지 열심히 똥꼬쇼를 하여 g(t)를 알아내었다. 총 정리하면,
( t ≤ -2 ) ... g(t) = 1
( -2 < t < -1 ) ... g(t) = 2
( t = -1 ) ... g(t) = 3
( -1 < t < 0 ) ... g(t) = 4
( t = 0 ) ... g(t) = 2
( 0 < t < 12 √ ) ... g(t) = 3
( t = 12 √ ) ... g(t) = 1
( t > 12 √ ) ... g(t) = 1
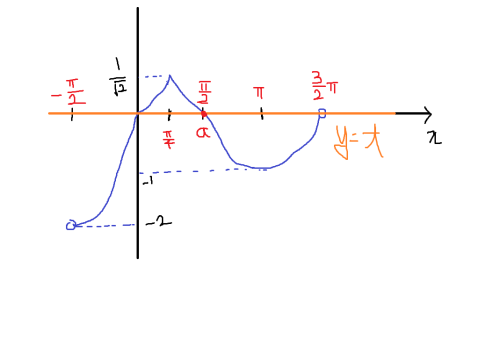
g(t)의 그래프를 그리면 다음과 같다.
다끝났다 씨발
이제 정답을 구해보자.
a, b, c를 각각 구해보면,
a = g(2 √2) = 1
b = g(0) = 2
c = g(-1) = 3
h(x)를 구해야하는데, g(t)의 함숫값이 틱장애마냥 1, 2, 3, 4 이지랄이다. h(g(t))는 연속이 되어야 하니까
h(1) = h(2) = h(3) = h(4)를 만족시켜야한다.
최고차항계수가 1인 사차함수라고 한다. 근데 등식을 세개밖에 못얻어서 h(x)를 확정하는건 불가능하다.
근데 여기서 구하라는 값이 h(a+5) - h(b+3) 빼기꼴이다. 하나쯤은 없어도 씹히겠다 생각을 하자.
인수정리로 묶어버리면
h(x) - h(1) = (x-1)(x-2)(x-3)(x-4)이다.
따라서 h(x) = (x-1)(x-2)(x-3)(x-4) + h(1) 이다.
위에서 구한 a, b, c 대입하고 싹 다 넣어버리면
h(6) - h(5) + 3 = 120 + h(1) - 24 - h(1) + 3 = 99
따라서 답은 4번이다.
평가[편집]
계산이 극혐인 문제긴 한데 이런 문제 몇번 풀다보면 패턴이 뻔하긴 하다. 그니까 그 뻔한패턴에 익숙해지도록 노력하는게 중요할 듯 하다.
눈치깠는지 모르겠지만 미분가능성 문제에서 계산을 수월하게 하기 위해서는 중요한 포인트가 있다.
평균변화율의 극한 lim(x->a)f(x) - f(a)x - a 딱 세우고
f(a) ≠ 0 이면 미분법 공식으로 가고,
f(a) = 0 이면 식변형을 통해서 극한값 계산으로 몰고간다.
그럼 아무리 어렵게 나온 문제도 앵간해선 다 푼다.