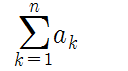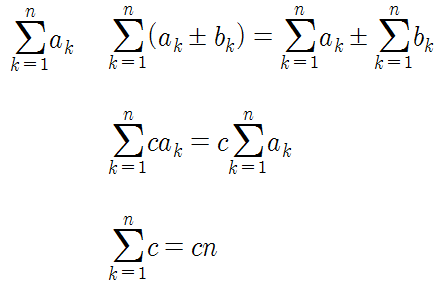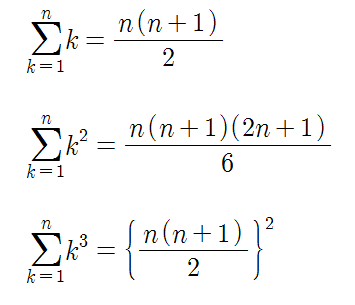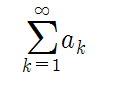급수

주의. 이 문서는 심히 진지하여 노잼일 수 있습니다. 이 글은 놀랍게도 조무위키에서 진지를 빨고 있습니다. 노잼이다 싶으시면 여기를 클릭하시어 이 문서를 탈출할 수 있습니다.

이 문서는 이과가 작성했거나, 또는 이과에 대해 다룹니다. 무슨 생각으로 작성한 건지는 잘 모르겠습니다만 맞는말임은 틀림 없습니다. 이과는 아다를 못 떼 마법을 쓰니까 말이죠...

이 문서는 문과는 이해할 수 없는 문서입니다. 이 문서는 문과생은 이해할 수 없습니다. 문과생은 팝콘이나 가져와라!

ㄴ그런데 수열과 급수는 문과 수능 범위고 이과는 논술 말고는 수열을 안보는 아이러니한 상황.....

이 문서는 이해하기 어려운 대상을 다룹니다. 이 문서는 일반적인 뇌를 가지고도 이해하기 어려운 대상에 대해 다룹니다. 두뇌를 풀가동해도 아마 이해하기 어려울 것입니다.

級數

• 상위 문서: 수열

개요

0.999...가 1임을 증명할 때 쓰는 것. 미적분I이니 문과충들도 배운다. 근데 등비급수 추가해줄 사람 있냐?

수학에서의 급수는 수열 a₁,a₂,a₃,...,a_n​​까지 주어졌을 때 이것들을 다 더해 a₁+a₂+a₃+...+a_n 로 나타낸 것, 즉 수열의 합을 의미한다. 급수의 예는 등차수열, 등비수열의 합, 자연수의 거듭제곱의 합 등이 있다. 급수는 수열을 제 몇 항까지 더하느냐에 따라 유한급수랑 무한급수로 나눌 수 있으며, 유한급수는 수학 법칙을 이용해 계산할 수 있는 반면, 무한급수는 극한을 이용해 계산해야 한다. 다만 모든 급수의 값을 구할 수 있는 것은 아니다.

급수를 표현할 때는 Σ(시그마) 를 이용하여 표현할 수 있다. 시그마란 문자를 쓰는 이유는 합을 의미하는 SUM에서 앞글자가 S이기 때문이라고 한다. (Σ는 영어로 S를 의미한다.)

급수의 생긴 꼬라지↓

이 꼬라지로 생겼다.

시그마 오른쪽에는 일반항을 써주자.

유한 급수

유한한 급수다.

자세히 말하자면 유한급수는 끝이 있는 수열의 합을 의미한다. 일반적으로 2015 현행 교육과정 기준으로 수학1에서 배우는 수열의 합은 여기에 포함된다. 유한급수의 일반적인 성질은 다음과 같다.

“

”

수1에 나오는 유한 급수(현행과정으론 수열의합에 나옴)와 관련된 공식. (디키가 책임지는 수학. 응?)

외워라 씨발.

근데 위의 공식은 고2때 배울거라 고3 올라와서 "저공식이 뭐지" 라고 생각하면 빨리 수1부터 다시 배우길 바란다.

더 빠른 방법은 수학을 포기하고 인생도 포기하면 된다.

문과도 이정도는 배워야 한다.

미적분 현행과정상 수열의극한을 배운다음 급수라는 단원부터 나온다. 거기선 수1에서 배운 수열의 합의 각종공식들을 질리게 활용하니 수1을 제대로 안했다면 다시 공부하길.(정적분의 활용에서도 사용)

밑에있는건 외울필요없다.

파일:5,6,7제곱 합.JPG

ㄴ 여기부터는 고등학교 과정 밖이다. 나온다 치면 구분구적법으로 풀라는 소리니까 급식들은 괜히 이런 데에 체력 소모하지 말자.

무한 급수

주의. 이 문서는 너무 난해합니다. 이 문서는 내용이 길거나 어렵거나, 병신 같이 싸지른 문서라서 정상인마저도 이해하기 어려운 문서입니다.

이 문서는 현재 '공.사.중' 입니다. 모두 힘을 합쳐 꼴리거나 찜찜한 부분이 있는 이 문서를 올바른 방향으로 바꾸어 나갑시다. (공사중인 문서이니, 이전으로 되돌리지 않으셔도 됩니다.)

무한급수는 끝이 없는 수열의 합을 의미한다. 유한급수와 달리 제 몇 항까지 더한다는 것이 없으며 끝까지 나아간다. 무한급수를 시그마를 이용하여 표현하면 시그마 위에 있는 숫자가 ∞로 바뀐다.

ㄴ개소리하고자빠졌다 더하는건 항상 유한번에서 끝난다 유한번 더한걸 극한때리는게 무한급수다

생긴 꼬라지.↓

ㄴ 무한대기호 왜 비대칭으로 보이냐
무한급수에서도 위 유한급수의 성질 1번, 2번은 각 급수가 수렴할 때 한해서 성립한다. 무한급수의 수렴에 대한 정확한 정의는 아래와 같다.

“

급수 의 n항까지의 부분합을 Sn으로 나타내보자. 이 때, 수열 {Sn}가 어떤 실수 S로 수렴할 때 급수가 수렴한다고 정의한다. 급수가 수렴하지 않으면 발산한다.

”

무한급수가 수렴하는지 발산하는지 확인하는 방법은 여러 가지가 있다. 하지만 판정법만으로는 수렴값을 구할 수는 없다...

고급수학에서는 초등함수는 집어치우고 이 새끼로 대신 함수를 표현한다. 초등함수로 적분이 안되는 게 너무나도 많기 때문이다.

무한급수의 수렴판정법

말그대로 급수가 수렴하는지 판정해주는 방법이다. 그런데 진짜 판정만 해줘서 수렴값을 구하려면 다른 방법을 동원해야 한다.

발산판정법 : 무한급수를 이루는 수열의 일반항의 극한값이 0이 아니면 발산한다. 예비검사라고 부르기도 한다. 극한값이 0이 나와도 아직 수렴한다는 보장은 없기 때문에, 더 검사해봐야 한다.

적분판정법 : 수열의 합도 수열로 나타낼 수 있다. 첫번째 항까지의 합, 두번째 항까지의 합, n번째 항까지의 합.......해서 말이다. 합으로 이루어진 이 수열 {Sn}을 매끄럽게 통과하는 함수를 하나 준 뒤, 무한대까지 적분하여 얻은 결과가 수렴하는지 발산하는지로 판단한다. 여기서 {Sn}을 기하학적으로 해석하면 가로가 1이고 세로가 주어진 함수의 함숫값인 직사각형들의 합이다. 구분구적법을 생각하면 편하게 이해할 수 있다. 단, 적분판정법을 제대로 증명하려면 완비공리와 단조수열정리를 알고 있어야 한다.

비교판정법 : 이미 수렴 또는 발산을 알고 있는 급수를 데려다가 비교해서 판정하는 방법이다. 함수만 주어지면 금방 할 수 있는 적분판정법과는 달리, 주어진 급수의 항들을 변형하는 센스가 필요하다. 자매품으로 극한비교판정법이 있다.

교대급수판정법 : 교대급수는 그 급수를 이루는 수열의 일반항의 부호가 왔다갔다 하는 수열의 합이다. 이 수열의 일반항의 절댓값이 아래로 유계이면서 극한값이 0이면 수렴한다.

비 판정법 : 수열 일반항의 비율을 가지고 판정하는 방법이다. n번째 항을 기준량, (n+1)번째 항을 비교량으로 정했을 때 이것의 절댓값의 극한을 L이라 하자. L<1이면 절대수렴, L>1이면 발산이다. L=1이면 판단 못한다. 자매품으로 근 판정법이 있다. 얘는 수열의 n번째 항에 절댓값 취한 걸 n제곱근해서 그 극한을 L이라 둔 뒤에 비 판정법처럼 판정한다.

위 판정법들의 증명은 어렵지는 않으나, 처음 본다면 굉장히 좆같을 수 있다. 스튜어트 미적분학 교과서에 쉽게 쓰여 있으니 참고하는 것도 나쁘지 않다.

라마누잔합이라고 발산하는 급수를 수렴값이 존재한다면 억지로 그 숫자를 나타내는 법이 있다.

다른의미의 급수

給水

물 공급 병신아. 이거 모르면 ㄹㅇ 바보다.